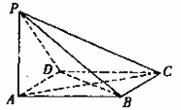
解：（解法一）：（1）设AC与BD交于O，连结PO。
∵底面ABCD是菱形，∴BD⊥AC，
∵PA⊥底面ABCD，BD
平面ABCD，
∴PA⊥BD，又PA∩AC=A，
∴BD⊥平面PAC。
又∵BD平面PBD，∴平面PBD⊥平面PAC。
（2）作AE⊥PO于E，∵平面PBD⊥平面PAC，∴AE⊥平面PBD，
所以AE为点A到平面PBD的距离。
在△PAO中，PA=2，
，
（3）作AF⊥PB于F，连结EF，∵AE⊥平面PBD，∴AE⊥PB，
∴PB⊥平面AEF，PB⊥EF，∴∠AFE为二面角A―PB―D的平面角，
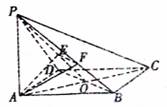
（解法二）：（1）设AC与BD交于O点，∵底面是菱形，∴AC⊥BD。
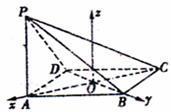
以OA、OB所在直线分别为x轴、y轴，以过点O且垂直平面ABCD的直线为z轴，
建立如图的空间直角坐标系，
则
，
，
∴平面PBD⊥平面PAC。
（2）设平面PDB的一个法向量为
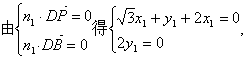
令
，
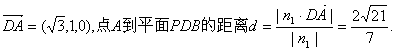
（3）设平面ABP的一个法向量
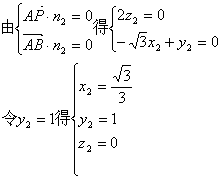
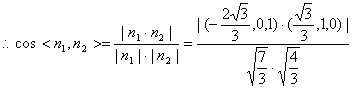
所以二面角A―PB―D的余弦值为
